
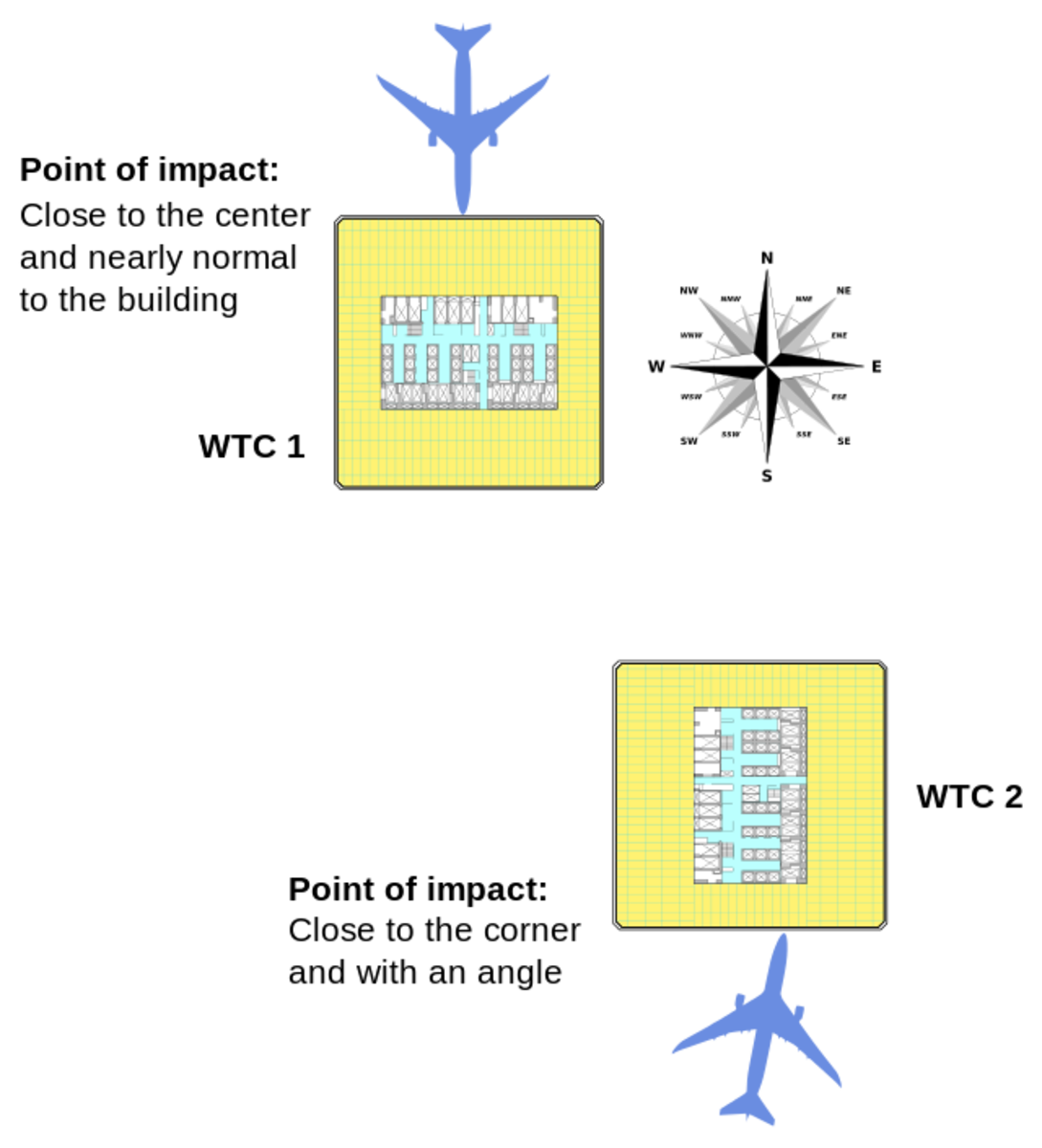
The Twins before the attack on September 11, 2001.
9/11 – Why Natural Collapse Was Mathematically Impossible
What Do You Think?
Was 9/11 an Inside Job?
Why Did They Collapse?
by Mario Buildreps (A graduate engineer. Become aware of topics in a way you have never heard before.
Soapboxie.com
It seems hard to prove that the collapse of the Twin Towers was an inside job.
From the few known facts it appears that the alleged buckling scenario has no mathematical basis, which implies that full collapse was impossible without introducing an unknown force in the core of the building.
Seismic recordings, from the closest by seismic recording station at Palisades, are often claimed as proof that explosives would be detonated just before the collapse. But this source cannot deliver any proof, because seismic activity prior to the major collapse does not prove the ignition of explosives. It is indirect, and therefore no direct proof.
The official version tells that the towers collapsed by the heat of the fire after the impact in combination with a damaged main structure. But how likely is it that this fire could cause a perfect full vertical collapse?
The collapse mechanism of the Twin Towers might look complicated to a layman. But it is not as difficult as it seems. Mathematics is the ultimate key to reveal the hidden truth.
- This article shows how much energy was released before and during the collapse.
- This article shows which forces were active just before and during the collapse.
- The calculations are accurate enough to draw conclusions from, that lead to an inevitable end conclusion.
- If you have no scientific background, this article will be too difficult to understand. (You can click the link that jumps to the bottom of this article.)
Facts and Figures Twin Towers
|
Item
|
Figure
|
|---|---|
|
Height
|
415 meters
|
|
Outside perimeter
|
63 x 63 meters
|
|
Inside support core
|
24 x 42 meters
|
|
Stories
|
110
|
|
Floor height (pitch distance)
|
3.77 meters
|
|
Basement
|
5 stories – 21 meters
|
|
Estimated empty weight (each tower)
|
475,000 metric tons
|
|
Estimated operational weight
|
565,000 metric tons
|
|
Specific average empty weight
|
1088 kg/m2
|
|
Floor space (each tower)
|
436,590 m2
|
|
Max wind load
|
225 km/h (140 mph)
|
|
Construction type
|
Steel / egg-crate
|
|
Earthquake proof
|
≤ Mag 5.0 (P-wave)
|
|
Natural (swing) frequency
|
11 sec.
|
|
Dampening construction
|
Visco elastic dampers, 100 per floor
|
|
Bomb attack
|
February 26, 1993 in basement -2
|
|
Airplane attack
|
September 11, 2001 centered on 81st and 95th floor
|
The Twin Towers Compared With Other Tall Skyscrapers

Facts and Figures of Other Skyscrapers
|
Tower
|
Stories Above Ground
|
Height* (m)
|
Weight** (kg/m2)
|
|---|---|---|---|
|
Willis Tower (Sears)
|
108
|
442
|
585
|
|
Burj Khalifa
|
163
|
584
|
967
|
|
Twin Towers
|
110
|
415
|
1088
|
|
Petronas Tower
|
88
|
452
|
1376
|
|
Taipei
|
101
|
448
|
1709
|
|
Empire State Building
|
102
|
381
|
1747
|
Specific Weight of Skyscrapers Varies
As you see in the above table the specific weight of skyscrapers varies, from light (Willis Tower) to heavy (Empire State Building). Skyscrapers are heavy at the base and light at the top. The average specific weight of a tower shows how solid the building is, which is also an indicator of its overall strength.
Most modern skyscrapers are resistant to S-waved earthquakes, which makes buildings swing like in heavy storms. Towers like the Taipei and Petronas are highly earthquake proof up to respectively 8.3 and 7.6. The Twin Towers were designed to deal with mild earthquakes of magnitude 5.0.
Adding mass to high towers is disadvantageous for the swinging characteristics, unless the additional mass outweighs the disadvantages in the form of strength and stiffness. Balancing between these two makes the design process of skyscrapers difficult.
The main principles of high towers are simple, the details and actual building extremely difficult.
Were the Twin Towers Earthquake Proof?
This is an important question, because it implies the dynamic strength of the tall skyscrapers.
The towers were designed to resist a combined S/P-waved earthquake up to magnitude 5. Buildings tend to be the most vulnerable to S-wave type earthquakes, especially when they are close to their natural frequency (Twin Towers 11 seconds).
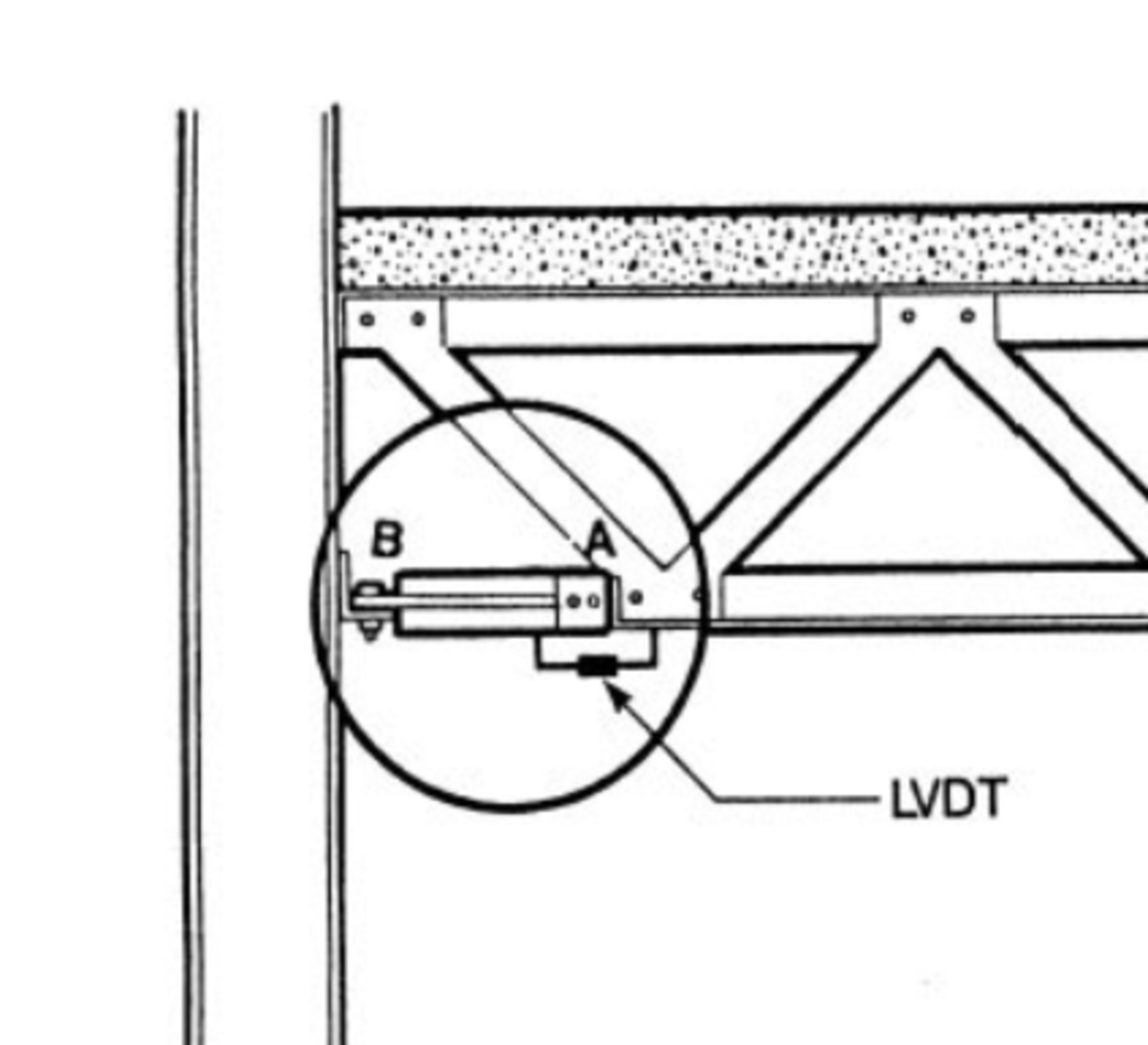
There were approximately 10,000 viscoelastic dampers installed in each tower to reduce wind-induced vibrations and S-waved vibrations from earthquakes. The earthquake of magnitude 4.0 in October 19, 1985 went by unnoticed. The towers had, as expected, no problem handling this, as most other buildings by the way.
The viscoelastic dampers as shown in the flanking picture absorb most energy released by an earthquake on a tower, which were evenly distributed from the 10thup to the 110th floor. What these dampers do is (partly) cancelling out destructive energy that might harm the construction.
A typical ground acceleration pattern where the tower were designed on was approximately 15% g – 1.5 m/s2.
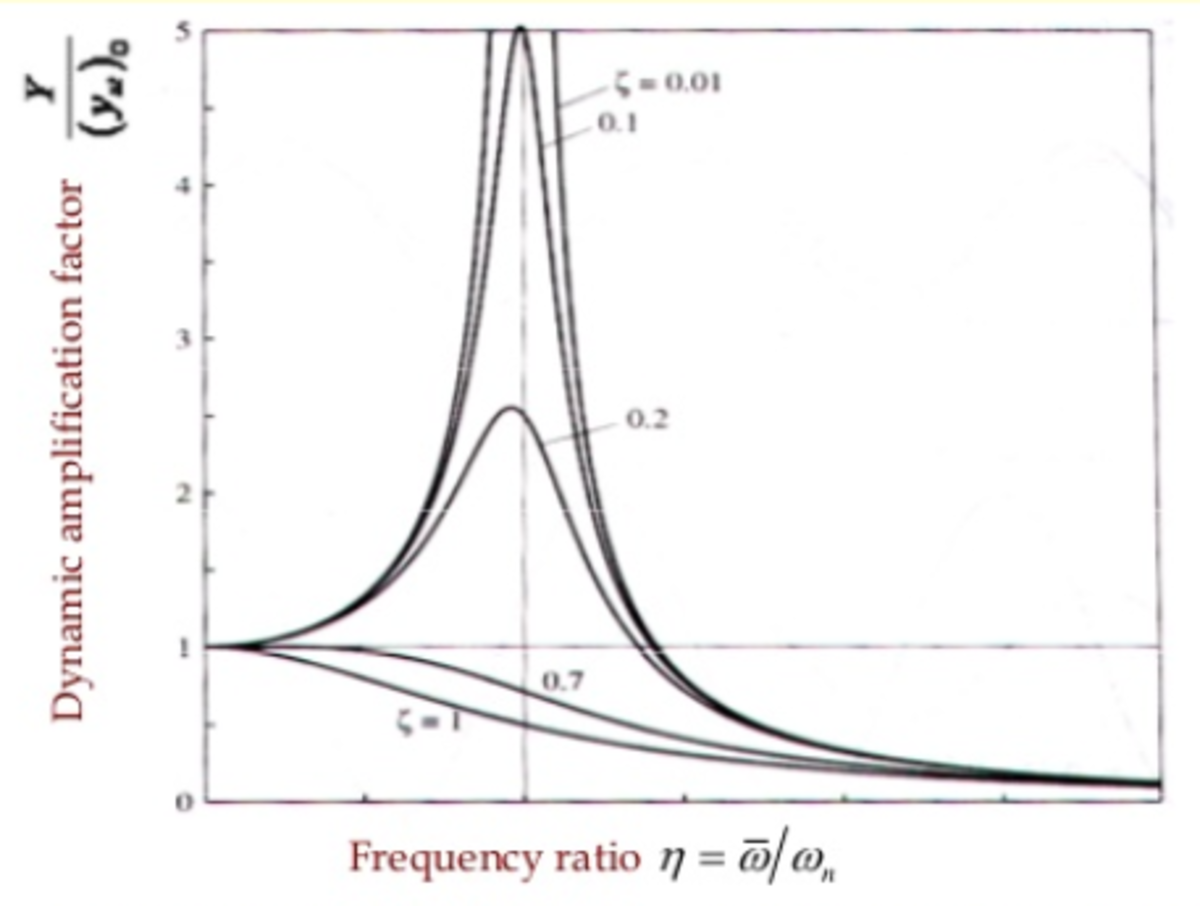
To find the correct dynamic load for welded steel constructions the maximum static load has to be divided by 2.65 (damping factor ζ=0.2). This is the so called Dynamic Amplification Factor (DAF). I left out the extensive calculations. The results:
- P-waves: +15% x 2.65 = 40%
- S-waves: +113% x 2.65 = 300%
- Combined P/S waves: (1.4 x 3) x 100% = 420%
Due to the earthquake resistance the construction could carry in static circumstances approximately 420% of the weight of the towers at ground zero level.
The Twin Towers had a specific design. The outer cage which gave the towers a specific look, acted as the major resistor against swinging. It made the towers extremely stiff. This high stiffness had consequences for the structure in the core, which had to take higher loads. The core structure had to be approximately 21% stronger.
This resulted in a building that was able to withstand 508% of its own empty weight in static situations.
Storm Resistance of the Twin Towers
This is an important factor in the case of 9/11, because it was a day with not much wind, which means that the full overcapacity in strength was available.
The towers were designed to handle wind speeds up to 225 km/h (140 mph). This is a dynamic load similar as with the horizontal motions (S-waves) during earthquakes. The maximum handleable wind load results in a force at the base that equals approximately 18% of its own weight.
This load is dynamic as well, which means it has to be factored with 2.65. The result is an extra required strength of 48%. Since earthquakes and wind load were possible to occur at the same moment, this was taken into account.
Total Static Strength
A usual safety factor in large constructions is 1.3.
The result is that the main structure of the towers at ground level were all together dimensioned at least:
- 978% (9.78 times) stronger than its weight in a static situation.
So due to all possible dynamical loads were the Twin Towers at base level capable to carry about 10 times there own weight in a static situation.
The Higher – The Less Strong
The main structure of the towers was at top level less strong constructed than at ground level. Material = Money. As a rule of thumb this formula is applicable for the Twin Towers:
- Vertical static strength Ps[n]max ≈ (9.78 – (9.78*(floor/110)) + 0.1) x 4.66 GN
- Vertical Dynamical Strength Pd[n]max = Ps[n]max / 2.65
- Static strength 81st floor Ps[81]max ≈ 12.5 GN (2.67 times own empty weight)
- Static strength 95th floor Ps[95]max≈ 6.7 GN (1.43 times own empty weight)
- Dynamic strength 81st floor Pd[81]max: 4.7 GN (1.01 times own empty weight)
- Dynamic strength 95th floor Pd[95]max: 2.5 GN (0.54 times own empty weight)
These figures are important in the collapse mechanism that is shown further on. The weight of the interior plays a role as well.
The formula will come at hand, later, when the dynamic collapse behaviour of the towers are regarded.
How Impact Proof Were the Twin Towers?
Empirical determination is the best way to find out the impact resistance of a building.
On February 26, 1993 a bomb exploded in the basement of 550 kg (TNT equivalent), which is equivalent to 2,3GJ. The explosion damaged 4 floors, together 16,000 m2(50,000 ft2). There was damage on floors just above and below the explosions. But there was no damage to the main structure that carried the full weight of the tower.
Based upon this event it is possible to determine the resistance of the building against explosions (impacts), which was at least 0.144 MJ/m2 in 15 ms[1] (the average horizontal blast time to nearby walls) at basement level. It indicates that the main structure could withstand 34.5 GJ/m2/hour. This is very high.
The basement was stronger than the rest of the tower. For the main support structure of high rise buildings counts the rule – the higher, the weaker.
The towers were constructed to handle an impact of a Boeing 707-320B flying at a speed of 907 km/h (607 mph), weighing 152,400 kg (336,000 pounds). The energetic equivalent of this is 4.8 GJ (1,160 kg TNT).
The Boeing 767 that hit tower 1 weighed about 180 metric tons and flew around 503 mph, which equals 225 m/s. The kinetic energy that this plane released onto a small part of the construction of the tower was 4.6 GJ.
The actual impact of the Boeing 767 on 9/11 was 96% of the design specifications, which indicates that the main structure at this height could be have been damaged. The exact amount of damage is not easy to determine, but by screening eyewitness statements, it is possible to determine the approximate amount of damage.
In both cases it appeared that the planes allegedly affected the main construction, covering 24,000 m2. Since the local main construction did not collapse under this impact energy means that the main structure was able to handle on floors 81 and 95at least 0.47 MJ/m2 in 245 ms[2] (this was the calculated duration of impact). This equals 6.9 GJ/m2/hour. This is also very high.
With these two impacts it is possible to determine the course (a graphic analysis) of the minimum impact resistability of the main structure: 34.5 GJ/m2/hour at basement level and 6.9 GJ/m2/hour at the 95th floor.
How Fireproof Were the Twin Towers?
The planes carried around 38,000 liters of kerosene (10,000 gallons), which had an energetic value of 1.6×1012 J (1,6 TJ). During the impact the liquid explosion spread over 6 floors which equals average 67.2 MJ/m2.
The towers were designed to handle a theoretical fire load of 220 MJ/m2/hour. The towers were constructed to handle this amount of energy, spread during 4 hours (cumulative 880 MJ/m2). When a fire becomes hot enough almost anything starts to burn, from paint to even aluminium. An average office contains 600 MJ/m2combustible materials.
The kerosene must have burned in less than 2 minutes (estimation), meaning that the permissible fire load of the towers could have been exceeded during the time the kerosene caught fire over 6 floors. With a short fire load of maximum 2,000 MJ/m2, the overload would be approximately 920%, assuming that all the kerosene burned inside the towers. But since a part of the kerosene exploded outside the towers means that it was less. How much less?
The volume of the fire ball around tower 1 during the hit was approximately 2,3×106m3. The fire ball could freely expand since the windows were already blown out. The total volume of the affected 6 floors was 9×104 m3. This means that around 5% of the kerosene burned inside the tower. Kerosene is so inflammable that it doesn’t burn up slowly. The perimeter of the explosion shows that there was no ‘place’ inside the building to burn this amount of kerosene.
Because only 5% of the kerosene burned inside the towers, means that the fire load was not more than 240 MJ/m2 during less than 2 minutes. The towers were able to handle this amount of energy easily. They were designed on this fire load, not just for 2 minutes but during 4 hours.
The heat of the fire after the impact was no problem. A kerosene fire of a few minutes doesn’t develop more heat than 600 °C – 700 °C (1110 °F – 1290 °F). The steel construction was coated with a heat resistant material, designed and applied to handle this heat for at least 4 hours. Whether the main structure at the height of impact was unaffected by this first heat burst is unsure, since the thermal isolation might have been damaged by the impact.
The kerosene was a spark that ignited a larger fire. Additionally, the blast of the liquid explosion blew away part of the combustible materials. That means it didn’t took part in the fire.
The total energetic value of the kerosene was a fraction of the energy necessary to bring the main structure in the danger zone. The kerosene plays hardly a role in the energetic balance, besides being the igniter of a much more dangerous fire – a burning office of 600 to 700 °C.
The towers were designed to handle this heat and fire load. Although parts of the protective coating might have been damaged due to the impact, which made the main structure vulnerable for the heat that followed.
Could the Aluminium Airplane Burn?
Maybe. Metal combustion is possible. Aluminium has a very high energy density of 31 MJ/kg, which is much more than TNT. Some explosives are based on the highly corrosive properties of aluminium, as well as some types of solid rocket fuel. Aluminium alloys show complicated mechanical, thermal and chemical behaviour.
Scientists observed several ignition processes of aluminium:
- aluminium can start to ignite at temperatures around 1,700 °C (3100 °F), when the protective oxide shell loses integrity.
- aluminium can start to ignite at temperatures around 1,150 °C (2100 °F), when the protective oxide shell shows mechanical cracks.
- aluminium can start to ignite at 650 °C (1200 °F) by shock waves which fractures the protective oxide shell.
The latter situation (3) could be the case in the 9/11 attacks, which would add a significant amount of energy to the fire.
A Boeing 767 contains around 70,000 kg aluminium (in several alloys). If this amount of aluminium burned in a short time it unleashed an amazing 2.2 TJ, spread over 6 floors and cause an additional average energy of 100 MJ/m2. At some points of the building an alleged aluminium fire could have been very concentrated and therefore fearsome. But the building was able to handle this heat and energy at that time. When aluminium starts to burn it does so very quickly. And when this heat source would have been responsible, it would have caused a collapse almost immediately after the impact.
So, there are no indications that burning aluminium would have been a major problem.
Even in the case the full aluminium body caught fire, the main structure of the building was still far from the danger zone of collapse, at least with an intact thermal isolation.
I heard three explosions, and then we heard like groaning and grinding, and tower two started to come down.
— Eyewitness Reports (911review.com)
Facts & Figures September 11, 2001
|
Item
|
Value
|
|---|---|
|
Mean wind speed / direction (origin)
|
11 km/h (7 mph) / NNW
|
|
Temperature
|
20 °C (68.1 °F)
|
|
Visibility
|
15 km (9.5 mi)
|
|
Time impact tower 1 (North)
|
8:46 AM
|
|
Time impact tower 2 (South)
|
9:03 AM
|
|
Height impact tower 1
|
95th floor
|
|
Height impact tower 2
|
81st floor
|
|
Time collapse tower 1
|
10:28 AM
|
|
Time collapse tower 2
|
9:59 AM
|
|
Impact-collapse time tower 1
|
102 minutes
|
|
Impact-collapse time tower 2
|
56 minutes
|
Required Collapse Energy
The towers were designed to handle:
- an air plane impact of similar size,
- a fire load of 3.5 GJ/m2.
The structural analysis done by Worthington, Skilling, Helle & Jackson is one of the most thorough calculations ever made for any building structure.
The amount of energy (up to 700 °C) each level could handle before collapsing was 14 TJ.
Required collapse energy:
- The impacts were centred on floor 81 and floor 95, spread over 6 floors.
- Tower 1 collapsed after 102 minutes over 6 floors – the necessary energy the fire would have to produce for this would be: 84 TJ (6 x 14), which equals 23.3 GWh (!)
- Tower 2 collapsed after 56 minutes over 6 floors – this also requires 84 TJ or 23.3 GWh.
- All possible energy together was: plane impact + kerosene + aluminium body = 4.6 GJ + 1,600 GJ x 5% + 2,200 GJ ≈ 2.3 TJ. This energy was applied from outside to inside. The thermal isolation was designed for much more.
- The only heat source that possibly could bring the construction in the danger zone was ignition of the aluminium body of the airplane. Especially in combination with a damaged thermal insulation.
- Nevertheless was the released energy on floor 95 of Tower 1 just 6% of the energy necessary to bring the main structure in the danger zone (2.3 / 14 x 35%) see table below.
- This energy was not equally spread over 6 floors. The impact on tower 1 was centred on floor 95. The spread was likely to be as in the table below. Floor 95 took 35% of the load.
- In both cases is over 90% of the energy missing to bring 6 floors altogether down.
- Even if the thermal insulation was damaged, doesn’t mean that all the thermal insulation was damaged.
Nevertheless looking at the facts – both towers collapsed, allegedly caused by the fires.
Around six floors were affected by impact and fire. The collapse would logically start at the floor that was the most affected by the fires – floor 81 and 95 of respectively tower 2 and tower 1. The main structure just above and below these floors was weakened but had more resistance, which was approximately in proportion with the rate of impact.
- Tower 2 collapsed towards the place of impact. This seems logical to me, which made me decide not to delve deeper into tower 2.
- Tower 1 collapsed in a strange way. The tower was impacted from the North side, while it initially started to collapse on the South side (check out the direction of the smoke when studying collapse videos, wind origin was NNW).
The collapse mechanism of tower 1 is fully illogical. I looked deeper into it and discovered interesting things and strange things, until I bumped onto mathematical impossibilities.
Impact Silhouette Tower 1
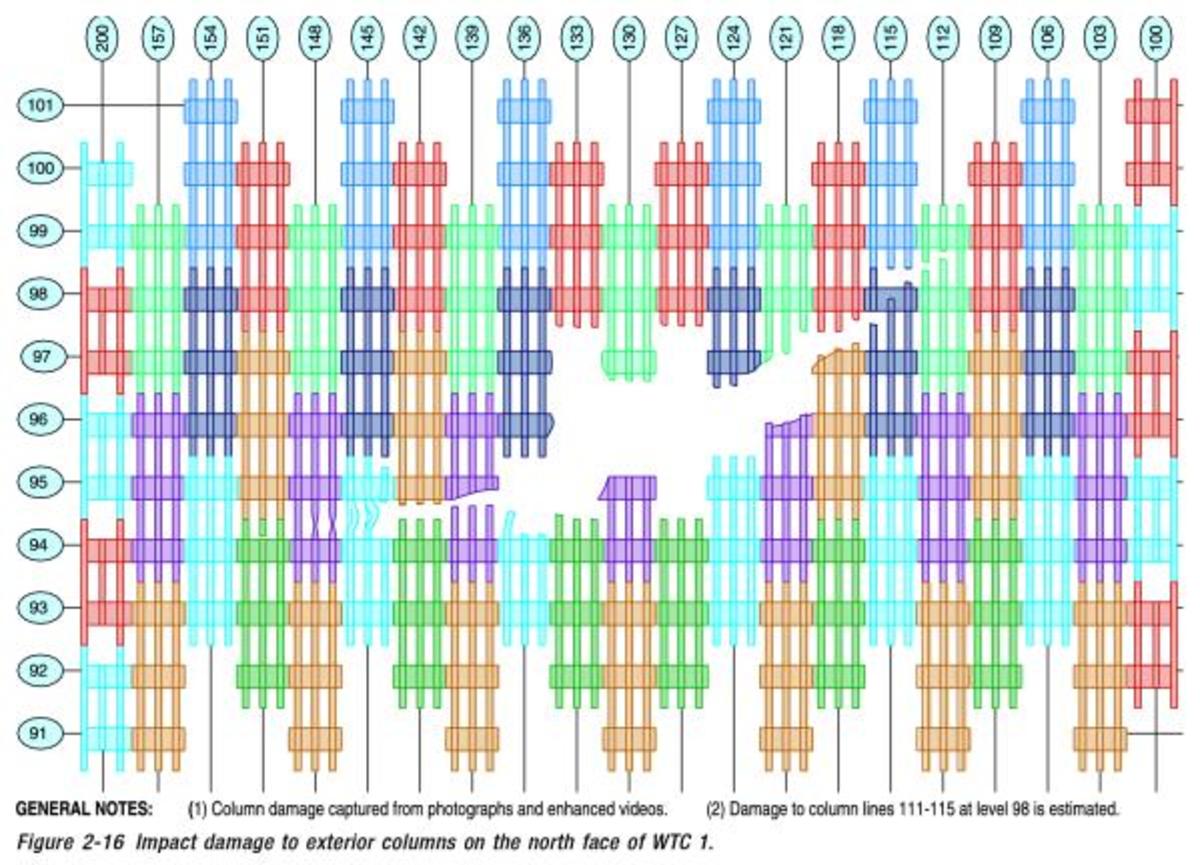
Estimated Impact Spread Tower 1
|
Floor Level
|
Amount of Absorbed Energy
|
|---|---|
|
93
|
5%
|
|
94
|
15%
|
|
95
|
35%
|
|
96
|
35%
|
|
97
|
7%
|
|
98
|
3%
|
The Official Version

Tower 1 – The Collapsing North Tower
The collapse of the North Tower (Tower 1) is strange. In the video below you must keep in mind that the airplane came from the right. The wind was coming from NNW. Now pay careful attention how it collapses.
- You see the tower first collapsing on the left side. This is the opposite side of impact. The construction was the most intact on precisely this side.
- At the moment the collapse starts you see flames coming from the right front side. This was the left side of impact. This indicates that there was only a fire on this side. It didn’t seem to burn anymore on the left side – the side of initial collapse – the opposite side of the impact. It nevertheless collapsed here first. It is strange.
Moment of Collapse Tower 1

The Dynamics of the Collapse Mechanism
There are many assumptions on the internet about what might have happened.
There are only a few facts:
- Tower 1 collapsed from top to bottom
- the collapse started at the top
- an intact block of 12 floors drops on the floors below that
- the 6 floors below seemed to have no resistance
- the remaining allegedly unaffected floors below have no resistance as well
- the whole tower collapses in about 12 seconds
- a ‘free’ fall from 415 meters would take about 10 seconds
The following technical events took place:
- The upper block of 12 floors that started to fall first, weighed 50,000 metric tons. Since there seems to be no resistance at all, the 12-floor block falls in almost ‘free fall’ acceleration and bumps onto the unaffected floors, starting from floor 92 and lower.
- The 12-floor block makes a free fall of 21.6 meters. The speed of this block at the moment it reached floor 92 was around 18 m/s. The kinetic energy of the 12-floor block was at that moment 8.1 GJ (energy=½mV²).
Regarding the construction of the tower, the following events should be expected:
- The main structure had to absorb this amount of energy which is converted into an increasing opposing force. The dynamic strength of the main structure at floor 92 was: Pd[92]max ≈ 3.0 GN.
- The highest possible deceleration of the main structure: a = Pd[92]max / mass = 57.9 m/s2. Time = 18/57.9 = 0.31 s.
- There was between the two colliding parts of the main structure a certain deformation zone.
- The smallest required deformation zone would be 2.78 meters to stop the 12-floor block. So, after 2.8 (9 feet) meters the building would stop to fall, which didn’t happen.
- The question is: why not? Is it possible that buckling was the critical factor?
The Likelihood of Collapse by Buckling

What is Buckling?
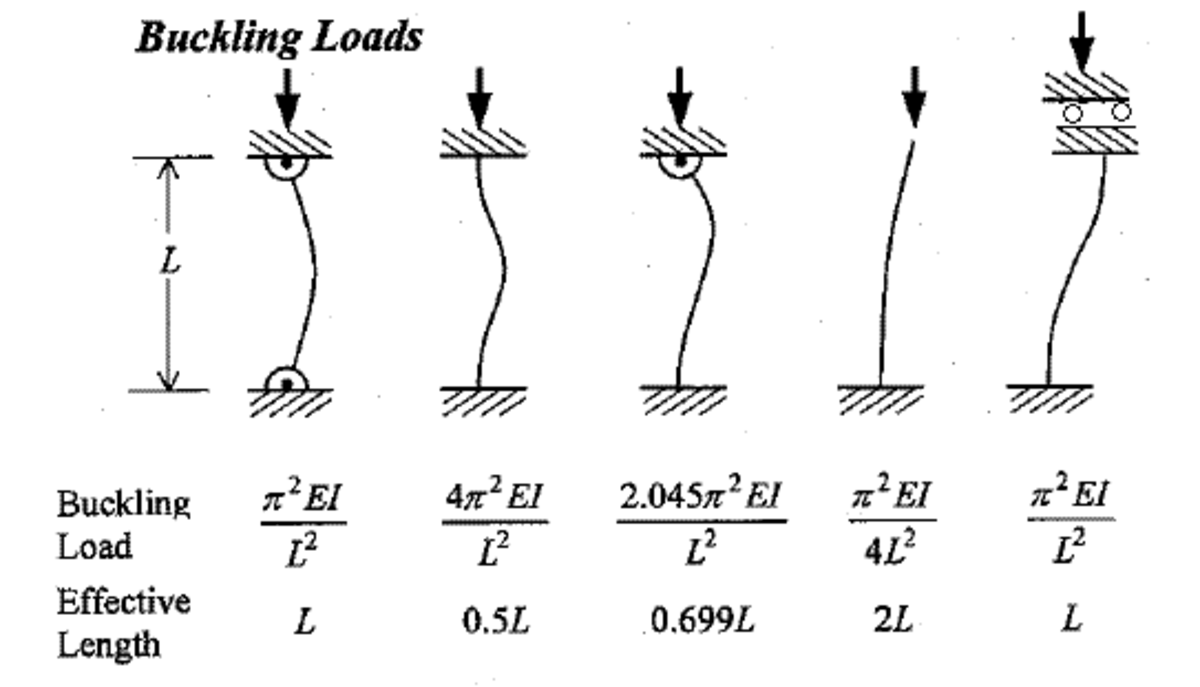
Buckling is serious stuff in engineering. Buckling is failure of a column that is subjected by a force in the lengthwise direction. The force at the point of failure is less than the ultimate force that the material is capable of withstanding. Buckling goes quadratical. A tube for example 1 meter length that buckles under a mass of 100 kg, will buckle under a mass of 25 kg if this same tube is 2 meters long.
Buckling gets increasingly complicated when columns are composed in a structure with a certain degree of interlocking between columns.
The buckling strength varies due to the way the beams are connected – fixed or rotatable. The buckling strength I calculated here is even the most unfavorable composition – rotatable.
Buckling
A team of engineers published in the Journal of Engineering Mechanics ASCE, Vol. 134 (2008), lead by Bažant, a research about the likelihood of buckling of the vertical structure of the Twin Towers. You will find similar reports of the same authors on the internet. I provided their report here.
The initial report about the alleged buckling of columns was already produced on September 13, 2001. Well, that’s very quick, isn’t it?
The authors created in their reports smokescreen, which in fact added no real value to the initial question: what caused the construction to fail?
The report makes illogical combinations like:
- “A meticulous investigation of unprecedented scope and detail”
- “not analyze the overall process of dynamic progressive collapse below the fire zone”.
- “Merely to get convinced of the inevitability of gravity driven progressive collapse, further analysis is, for a structural engineer, superfluous”.
This report does not even do what it promises to do, which would be a thorough examination of the reason of collapse by buckling, on the contrary, like already said, it creates only a smokescreen.
Furthermore they stated that structural analysis was superfluous. Why? The essence is in the analysis of the structure and the reason of collapse.
The report finishes with the conclusion that the buckling process will start approximately when a falling upper part falls 1 story.
- Tower 1: The critical falling distance is 4.2 meters,
- Tower 2: The critical falling distance is 2.9 meters.
If that would be true, the towers would collapse already under a light wind load.
After 15 pages full of nonsense they tell you “Several of the parameters of the present mathematical model have a large range of uncertainty“. How large? And how does this uncertainty works out on the critical falling distance? Silence…
There is a relative simple way to calculate what happened during the collapse. The static buckling strength of the weakened floors at the moment of collapse, regarding the amount of heat and damage, show accurately the static buckling strength of the ‘healthy’ building below.
How? Just a fraction before the collapse there is a state of perfect static balance.
Balance Situation at the Moment of Buckling
- Just before Tower 1 collapses this moment can be considered as a balance situation. This concept is crucial to understand. The weight of the 12-floor block is in static equilibrium with the counterforce of the construction that is about to collapse or buckle.
The moment Tower 1 Collapsed:
- Official reports state that the average heat of the fire was not more than 650 °C. Let’s take this as a starting point. This temperature is also reported by the NIST, see page 161 chapter 7.1. The elastic modulus of steel at 650 °C is 32%. At 20 °C it is much stronger – 210,000 MPa (100%).
- The collapse starts at the moment the remaining weakened structure is not able to carry the load anymore – the 12-floor block above the fire.
- The outer structure (the façade) lost due to the airplane impact 23% of its strength, leaving 77% to support the 12 floors block above.
- How much integrity the inner core lost has to be estimated. According to eyewitness reports the plane didn’t fully penetrated the vertical beams. Nevertheless at least 6 of the 8 front row columns (total 24 outer columns on the inner core, the other inner columns were used to carry elevators, etc.) that carried the floors along the inside perimeter must be regarded as lost as floor carriers by the impact of the plane. 75% of the original support was left.
- Euler’s formula says: F = (π2 × E650 × I)/ L2. The weight of the 12-floor block that lies on top of the damaged construction can be regarded as ‘F’. The whole mechanism at the moment of collapse can be reduced to this formula.
- According to the formula of Euler, the composed buckling strength of the tower at level 95 just before the moment of collapse was: (π2 × E650 × I) / L2 = Weight12-floorblock. Where ‘E650‘ is the elasticity modulus of steel at 650°C.
- Itower1at650 = (Weight12-floorblock × L2 ) / (π2 × E650) = (500,000,000 N × 12.96 m2) / (9.86 × (32% × 210,000)) = 9,780 m4. This value is the composed area moment of inertia just before the moment Tower 1 collapsed.
- The unaffected floors below the impact can be derived from 7. There were only two variables left that were different: temperature (20°C) and the amount of damage.
- Temperature: The elasticity modulus of steel at 650°C is 32% of the elasticity modulus of steel at 20°C. This means that the buckling strength of steel at 650°C is also 32% (linear). The buckling strength of steel at 20°C is 3.125 higher than at 650°C (E20 ÷ E650 = 100% ÷ 32%).
- Amount of damage: The floor that started to buckle first had an estimated damage of 25% in the core and 23% on the façade. The floor load was approximately equally distributed over both supporting structures (50% inner and 50% façade). That means that the remaining support construction can be derived from 100% – ((25+23) ÷ 2) = 76%. The weight of the upper floors was carried by 76% of the remaining structure, which was also weakened by the heat.
- At the moment of collapse the undamaged, unaffected structure below had a static load capacity that was: 3.125 × (100% ÷ 76%) = 4.1 times higher.
- The buckling strength of the healthy building can be derived by: Itower1at20 = Itower1at650 × 4.1 = 40,098 m4.
- Thus, the static resistance against buckling of the healthy floor 92 and 91 was 410% the strength of the floors that actually collapsed.
- The dynamic strength of floor 92, was according to eyewitness reports not damaged. The dynamical strength (DAF) is 2.65 times less as the statical strength. This results in an overcapacity against collapse of 155% (4.1 ÷ 2.65). Which was beyond the safety factor of 1.3.
- This means the main structure below (floors 92, 91, 90) had to stop the fall by definition. No doubt about it.
Conclusion: Full collapse by buckling is mathematically impossible.
What Does This Prove?
- That the towers could not collapse by itself. Impossible. Logically if the inner core structure would be vaporized in an instant, only 75% of the resistance against buckling would remain. The façade was not able to carry the load by its own. That would mean a full collapse of the tower in an amazing speed. Which it did.
This clearly proves that also a ‘natural’ buckling was impossible.
- The worst case ‘natural’ situation would be a tower that was 25 meters (82 feet) shorter.
So, this proves in several ways that natural collapse was impossible.
The inevitable conclusion is that a full collapse wasn’t possible without a destructive interference in the core structure. And that is a horrible conclusion.
Conclusion – Why Did the Twin Towers Collapse?
There are a few consistent conclusions to make.
- The towers were designed to handle the airplane impact, the heat and the fire load. But this doesn’t prove they were actually capable to withstand an impact. It’s mere an indication.
- 95% of the energy to weaken the structure enough to cause full collapse was not available. But the main structure collapsed in both cases. Why?
- The 12-floor block of Tower 1 must have stopped to drop 2.8 meters (9 feet) below floor 92, but it didn’t. There is no reason why it should continue to drop, for the main structure was tough enough to absorb the energy of the 12-floor falling block.
- The main structure below floor 92 was fully intact, able to stop the falling 12-floor block of Tower 1.
- Technically spoken Tower 1 should have been about 25 meters (82 feet) shorter.
- Buckling was not an option as I showed with mathematics above.
Why did the towers collapse? Regarding from a technical perspective this was impossible without adding another energy source to it.
The aluminium of the airplane contained too less energy to cause a melt down of the construction, whatever source might claim about this – it is nonsense. Furthermore was the construction strong enough to stop the falling 12-floor block as mathematically proved.
How much energy was necessary to make the towers collapse? The absolute minimum amount of energy to bring the towers down is the average dynamic strength Pd[55]max at floor 55 × the mid-height of a tower, 207 meters. This results in at least 1.8 TJ, only when this energy would be injected within a few milliseconds into the vertical core beams. That means, from the inside. An intense heat which easily bypassed the thermal isolation.
1.8TJ is an unimaginable amount of energy, which equals the energy of over 200 thunderbolts. The speculations of the Russians that a small nuclear device was detonated in the core seems to be not unthinkable, especially because natural collapse was impossible. The intense heat of 4000 °C of a nuclear device is enough to bypass the thermal isolation in an instant flash over the full height.
The result? A full collapse like a house of cards, allegedly caused by airplane impacts operated by bearded goat herders. Of course, that sounds likely. That so many believe this says something about the current human condition.
Other sources speak of thermite and even thermane which is even more vicious than thermite. This is also possible. But what is impossible is that these buildings collapsed under their own weight. It was a well calculated and orchestrated action.
We all know what happened after 9/11 – George Orwell’s ‘1984‘ started to unfold.
Sources
- [1] Blast Mitigation Information from Graham Architectural Products.
- [2] Based on Boeing’s spec’s – impact time derived from cruise speed and length of the plane.
- other sources: Eduardo Kausel / Gregory H. Urich / Thomas W. Eagar and Christopher Musso.
© 2014 Buildreps
___
http://soapboxie.com/us-politics/Twin-Towers-Why-Did-They-Collapse